I learned how to use Python’s cProfile module last week and thought it was pretty cool. So at work this week when we came across a couple across a couple of lines at code I thought could be optimized I used it as an opportunity do a little profiling.
I compared loops against list comprehensions and then against the set object. I knew loops would be slower in both cases, but like a homework problem I wanted to go through the steps and get a better handle on numbers.
Comprehension vs Loops
I started by comparing a list comprehension against an equivalent for loop to pull all the even numbers out of the first 10,000 integers.
def lists_with_for_loop():
evens = []
for item in range(10000):
if item % 2 == 0:
evens.append(item)
def lists_with_comprehensions():
evens = [x for x in range(10000) if x % 2 == 0]Here are the results:
| function | ncalls | tottime | percall | cumtime | percal |
|---|---|---|---|---|---|
| lists_with_for_loop | 1 | 0.013 | 0.013 | 0.022 | 0.022 |
| lists_with_comprehensions | 1 | 0.002 | 0.002 | 0.002 | 0.002 |
List comprehensions win by about an order of magnitude.
Sets vs Loops
To compare sets and loops I made a loop that generated a list of all the unique entries in a list of 10,000 integers between 0 and 1,000. It occurred to me that this was a relatively “sparse” case so I also made a “dense” one where the integers are distributed between 0 and 10. Here is the code:
SPARSE_INPUT_LIST = N.random.random_integers(0,1000,10000)
DENSE_INPUT_LIST = N.random.random_integers(0,10,10000)
def unique_with_for_loop_dense():
output = []
for item in DENSE_INPUT_LIST:
if item not in output:
output.append(item)
def unique_with_for_loop_sparse():
output = []
for item in SPARSE_INPUT_LIST:
if item not in output:
output.append(item)
def unique_with_set_dense():
output = set(DENSE_INPUT_LIST)
def unique_with_set_sparse():
output = set(SPARSE_INPUT_LIST)And here are the results:
| function | ncalls | tottime | percall | cumtime | percal |
|---|---|---|---|---|---|
| unique_with_for_loop_sparse | 1 | 0.515 | 0.515 | 0.518 | 0.518 |
| unique_with_set_dense | 1 | 0.024 | 0.024 | 0.024 | 0.024 |
| unique_with_for_loop_dense | 1 | 0.013 | 0.013 | 0.013 | 0.013 |
| unique_with_set_sparse | 1 | 0.008 | 0.008 | 0.008 | 0.008 |
So sets always beat loops, but the difference is more dramatic the sparser the input list is. This makes sense since the set object uses a hash table while the for loop I write just does a list look up (though I’m not exactly sure how it’s implemented). The larger the output list/set will be the more efficient the hash is over the list.
I made a plot of this for a a non-negative set of 1,000,000 integers of varying densities.
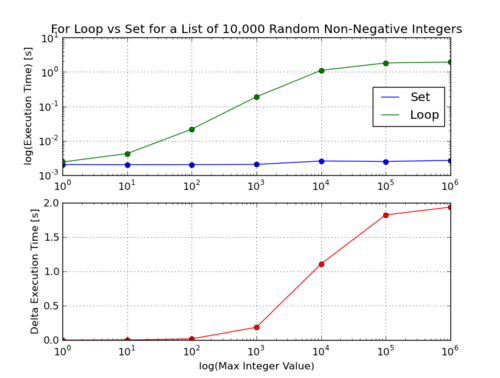
A couple of notes:
-
The bench marks and the plots were generated on different computers so the numbers don’t match up, though the trends should be the same. I just didn’t feel like entering all the numbers in the html
tabletags again. -
To generate the plot I used the
timemodule and took the difference of two time instances to find the run time. -
You can view the source code for the benchmarks and the plot (and any other future code from this blog) on my Github Page